Métodos de resulución
Si bien para los sistemas de ecuaciones lineales existen multitud de técnicas del álgebra lineal, para los sistemas de ecuaciones no lineales el problema es técnicamente más difícil.
Los métodos analíticos se restringen casi exclusivamente a sistemas de ecuaciones lineales. Ni siquiera se conoce una solución analítica para el sistema de ecuaciones de segundo grado general:
Las aplicaciones técnicas generalmente recurren a algoritmos numéricos que permiten calcular aproximaciones numéricas a las soluciones de un sistema de ecuaciones.
Uno de los métodos numéricos que puede generalizarse a sistemas no lineales es el método de Newton-Raphson. En el caso multidimensional la resolución numérica del sistema de n ecuaciones 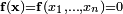 puede hacerse a partir del conocimiento de una solución aproximada
puede hacerse a partir del conocimiento de una solución aproximada  , siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
, siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
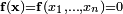 puede hacerse a partir del conocimiento de una solución aproximada
puede hacerse a partir del conocimiento de una solución aproximada  , siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
, siempre y cuando la aplicación anterior sea diferenciable, mediante el esquema iterativo:
O más explícitamente:
Lamentablemente la convergencia del esquema iterativo anterior no está garantizada y en casos de soluciones múltiples la convergencia puede darse hacia la solución no deseada.
Métodos gráficos
Los métodos gráficos son didácticos e ilustrativos, aunque en general carecen de interés práctico en las aplicaciones técnicas de importancia. Además están restringidos generalmente a sistemas de dos o tres ecuaciones reales.
Dos sistemas de ecuaciones con dos incógnitas de valor real, suelen aparecer como uno de los cinco tipos diferentes mencionados a continuación. 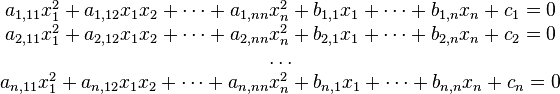
![\mathbf{x}^{(m+1)} = \mathbf{x}^{(m)} - [D\mathbf{f}(\mathbf{x}^{(m)})]^{-1}(\mathbf{f}(\mathbf{x}^{(m))}), \qquad \mathbf{f}:\R^n \to \R^n,\ \mathbf{f}\in C^{(1)}(\R^n;\R^n)](https://upload.wikimedia.org/math/8/f/b/8fb6bc36a0d7848d6c942dbd8a4ad727.png)
0 comentarios:
Publicar un comentario